Statistik
Das arithmetische Mittel
Anstatt arithmetisches Mittel sagt man auch häufig Durchschnittswert oder Mittelwert. Du berechnest das arithmetische Mittel indem du die Summe aller Werte durch die Anzahl der Werte dividierst.

Beispiel:
In einer Klasse mit 20 Kindern wurden bei einem Test folgende Noten vergeben:
1, 2, 2, 4, 2, 1, 3, 2, 4, 5, 3, 3, 2, 1, 2, 2, 4, 5, 2, 2
arithmetisches Mittel = (1+2+2+4+2+1+3+2+4+5+3+3+2+1+2+2+4+5+2+2) : 20 = 52 : 20 = 2,6
Das gewogene arithmetische Mittel
Das gewogene oder gewichtete arithmetisches Mittel erleichtert oft die Berechnung des Mittelwertes. Du berechnest das arithmetische Mittel indem du zuerst die Werte (x) mit ihrer Häufigkeit (h) multiplizierst. Die Summe aus diesen Multiplikationen wird auch hier wieder durch die Anzahl der Werte dividiert.

Beispiel:
In einer Klasse mit 20 Kindern wurden bei einem Test folgende Noten vergeben:
1, 2, 2, 4, 2, 1, 3, 2, 4, 5, 3, 3, 2, 1, 2, 2, 4, 5, 2, 2
gewogenes arithmetisches Mittel = (1·3+2·9+3·3+4·3+5·2) : 20 = (3+18+9+12+10) : 20 = 52 : 20 = 2,6
Der Zentralwert (Median)
Der Zentralwert (auch Median genannt) ist der Wert in der Mitte einer der Größe nach geordneten Liste (Rangliste). Deshalb müssen zuerst alle Werte der Größe nach geordnet werden (Rangliste). Der Wert in der Mitte ist der Zentralwert (Median).
- Wenn die Anzahl der Werte ungerade ist, ist die mittlere Zahl der Zentralwert (Median).
- Wenn die Anzahl der Werte gerade ist, werden die beiden mittleren Werte addiert und anschließend durch 2 dividiert.
Beispiel:
In einer Klasse mit 20 Kindern wurde ermittelt wie viel Taschengeld die Kinder monatlich erhalten. Dabei wurden folgende Werte ermittelt:
10 €; 50 €; 12 €; 50 €; 20 €; 5 €; 100 €; 10 €; 20 €; 30 €; 40 €; 20 €; 20 €; 10 €; 12 €; 17 €; 20 €; 60 €; 185 €; 5 €
- Rangliste erstellen (Werte der Größe nach ordnen):
5; 5; 10; 10; 10; 12; 12; 17; 20; 20; 20; 20; 20; 30; 40 ; 50; 50; 60; 100; 185 - Der Wert in der Mitte ist der Zentralwert (Median)
5; 5; 10; 10; 10; 12; 12; 17; 20; 20; 20; 20; 20; 30; 40 ; 50; 50; 60; 100; 185
Wenn die Anzahl der Werte gerade ist (20 Kinder) werden die beiden mittleren Werte addiert (20+20=40) und durch 2 dividiert (40:2=20)
Der Zentralwert (Median) ist nicht so genau wie das arithmetische Mittel. Wenn es aber "Ausreißer" (sehr kleine oder sehr große Werte) in den Werten gibt, ist der Median im Vorteil, da er weniger empfindlich gegen "Ausreißer" ist.
Der Modalwert
Der Modalwert (m) oder auch Modus ist der am häufigsten vorkommende Wert der Rangliste.
Beispiel:
In einem Kleinbetrieb mit 5 Mitarbeitern wurden die Fehlstunden der Mitarbeiter notiert. Am Ende eines Jahres wurden folgende Werte ermittelt:
- Mitarbeiter A: 12 Stunden
- Mitarbeiter B: 10 Stunden
- Mitarbeiter C: 65 Stunden
- Mitarbeiter D: 10 Stunden
- Mitarbeiter E: 43 Stunden
Der Modualwert ist 10. Es ist der am häufigsten vorkommende Wert in der Liste.
Das Minimum und das Maximum
Das Minimum und das Maximum bezeichnen den kleinsten und den größten Wert einer Liste.
- Das Minimum ist der kleinste Wert einer Rangliste
- Das Maximum ist der größte Wert einer Rangliste
Beispiel:
In Vorarlberg gibt es 4 Bezirke. Die Fläche der Bezirke ist unterschiedlich groß.
- Bludenz: 1.286 km²
- Bregenz: 865 km²
- Dornbirn: 172 km²
- Feldkirch: 278 km²
Minimum = 172
Maximum = 1286
Die Spannweite
Die Spannweite ist der Abstand zwischen dem größten und dem kleinsten Wert einer Liste.
Spannweite = Maximum - Minimum
Beispiel:
In einer Familie mit 3 Kindern wurde das Alter der Familienmitglieder notiert:
- Mutter: 46 Jahre
- Vater: 48 Jahre
- 1. Kind: 18 Jahre
- 2. Kind: 16 Jahre
- 3. Kind: 13 Jahre
Spannweite: 48 - 13 = 35
Das erste, zweite und dritte Quartil
Quartil bedeutet übersetzt Viertelwert. Das erste, zweite und dritte Quartil unterteilen eine Rangliste in vier gleich große Abschnitte. Der Zentralwert (Median) ist der Wert in der Mitte einer Rangsliste. Deshalb sind der Zentralwert und das 2. Quartil identisch.
Der Zentralwert bzw. das 2. Quartil teilt eine Rangliste in zwei gleich große Hälften (untere Hälfte und obere Hälfte).
- Das 1. Quartil ist der Zentralwert der unteren Hälfte
- Das 3. Quartil ist der Zentralwert der oberen Hälfte
Beispiel:
Bei einem Sportfest wurden die Sprungweiten der einzelnen Kinder gemessen und notiert (alle Angaben in Zentimetern):
435; 420; 485; 440; 490; 430; 425; 510; 500; 480; 460
Aufgaben:
- Erstelle eine Rangliste
- Ermittle das Minimum, das Maximum und die Spannweite
- Ermittle den Zentralwert bzw. das 2. Quartil
- Ermittel das 1. und das 3. Quartil
Lösung:
- Rangliste erstellen (Werte der Größe nach ordnen):
420; 425; 430; 435; 440; 460; 480; 485; 490; 500; 510
- Minimum, Maximum und Spannweite ermitteln:
Minimum = 420
Maximum = 510
Spannweite = Maximum - Minimum = 510 - 420 = 90
- Zentralwert bzw. 2. Quartile ermitteln:
420; 425; 430; 435; 440; 460; 480; 485; 490; 500; 510
Zentralwert bwz. 2. Quartil = 460
- Erste und Dritte Quartile ermitteln:
420; 425; 430; 435; 440; 460; 480; 485; 490; 500; 510
1. Quartil = 430
3. Quartil = 490
Das Boxplot-Diagramm
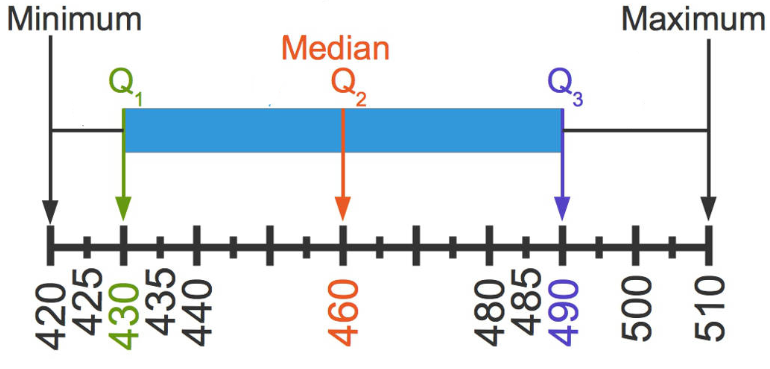
Das Boxplot-Diagramm oder auch Kastendiagramm besteht aus einem Rechteck (Box) und zwei Antennen (Whisker).
- Das Rechteck (Box) wird zwischen dem unteren Quartil (1. Quartil) und dem oberen Quartil (3. Quartil) eingezeichnet.
- Von dieser Box führt eine Linie nach links bis zum Minimum und eine Linie führt nach rechts bis zum Maximum.
- Der Zentralwert (Median) bzw. das 2. Quartil wird mit einer senkrechten Linie in die Box gezeichnet.
Hier findest du eine Präsentation zum Thema Statistik.
Interaktive Aufgaben
Hier findest du Verweise zu interaktiven Aufgaben zu folgenden Themen: