Funktionen
- Eine Funktion ist eine eindeutige Zuordnung zwischen zwei Größen
- Jedem Wert der ersten Größe wird GENAU EIN WERT der zweiten Größe zugeordnet.
- Die erste Größe wird mit x bezeichnet (unabhängige Größe)
- Die zweite Größe wird mit y bezeichnet (abhängige Größe)
- Die Menge aller Werte für x nennt man Definitionsmenge (D)
- Die Menge aller Werte für y nennt man Wertemenge (W)
Wertetabelle und Funktionsgraph
Jede Funktion kann durch eine Wertetabelle oder ein einen Funktionsgraphen dargestellt werden.
Beispiel:
Funktionsgleichung:
y = 2 · x + 3
Wertetabelle:
x | -2 | -1 | 0 | 1 | 2 |
y | -1 | 1 | 3 | 5 | 7 |
Funktionsgraph:
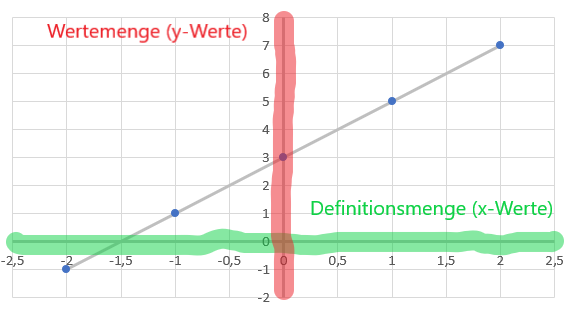
Lineare Funktion
Die allgemeine Form einer lineare Funktion wird durch folgende Funktionsgleichung angegeben:
y = k · x + d
y...Wertemenge
x...Definitionsmenge
k...Steigung der Funktion
d...Abschnitt auf der y-Achse
- Der Graph einer linearen Funktion ist immer eine Gerade.
- Die Steigung der Funktion (steigend oder fallend) wird durch den k-Wert angegeben.
- Der d-Wert gibt an, an welcher Stelle der Graph der Funktion die y-Achse schneidet.
Beispiel:
Funkionsgleichung:
y = 3 · x - 2
Funktionsgraph:
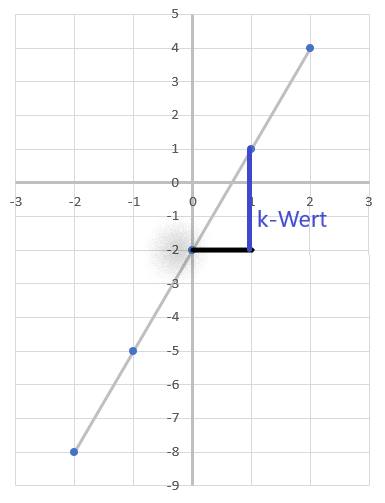
Homogene lineare Funktion
- Der Graph einer homogenen linearen Funktion ist eine Gerade die durch den Koordinatenursprung (0/0) geht.
- Der d-Wert einer homogenen linearen Funktion ist 0
Beispiel:
Funkionsgleichung:
y = 1,5 · x + 0 => y = 1,5 · x
Funktionsgraph:

Inhomogene lineare Funktion
- Der Graph einer inhomogenen linearen Funktion ist eine Gerade die NICHT durch den Koordinatenursprung geht.
- Der d-Wert einer homogenen linearen Funktion ist größer oder kleiner als 0.
Beispiel:
Funkionsgleichung:
y = 2· x + 1
Funktionsgraph:

Quadratische Funktion
Die allgemeine Form einer quadratischen Funktion wird durch folgende Funktionsgleichung angegeben:
y = a · x² + b · x + c
y...Wertemenge
x...Definitionsmenge
a...öffnet den Funktionsgraphen nach unten oder oben und streckt oder staucht den Funktionsgraphen
b...verschiebt den Funktionsgraphen sowohl in die x-Richtung als auch in die y-Richtung
c...verschiebt den Funktionsgraphen nach oben oder unten
Beispiel:
Funkionsgleichung:
y = 1· x²
a-Wert = 1
b-Wert = 0
c-Wert = 0
Funktionsgraph:

Hier kannst du eine quadratische Funktion beliebig verändern.
Onlineübungen
Hier kommst du zu einem Lückentext zum Thema Funktionen.